Bilangan Eksponen
Bimbingan Belajar29. Bilangan Eksponen ialah bentuk suau bilangan perkalian dengan bilangan yang sama kemudian di ulang-ulang atau pengertian singkatnya adalah perkalian yang diulang-ulang.
Bilangan Eksponen biasa digunakan secara luas di berbagai bidang seperti: dalam bidang ekonomi, biologi, kimia, fisika, dan ilmu komputer dengan aplikasi seperti perbungaan, pertumbuhan jumlah penduduk, kinetika kimia, perilaku – perilaku gelombang dan kriptografi kunci publik atau ilmu yang mempelajari tentang bagaimana agar pesan atau dokumen seseoarang aman tidak terbaca oleh orang lain yang tidak berhak membacanya.
Contoh:
$a^{n}$ = a x a x a x…x a dikalikan sebanyak jumlah n
Contoh angkanya:
$2^{5}$ = 2x2x2x2x2 hasilnya 32
Sifat-Sifat Bilangan Eksponen
Terdapat beberapa sifat yang bisa kita ketahui didalam memahami bilangan eksponen yaitu di antaranya:
Pertama:
$a^{m}\times a^{n}=a^{m+n}$ apabila dikali maka pangkatnya harus ditambah
Contoh: $5^{2}\times 5^{3}=5^{2+3}=5^{5}$
Kedua:
$a^{m}\div a^{n}=a^{m-n}$ apabila dibagi maka sebaliknya pangkatnya harus dikurang
Contoh:
$5^{5}\div 5^{3}=5^{5-3}=5^{2}$
Ketiga:
$\left ( a^{m} \right )^{n}=a^{m\times n}$ apabila di dalam kurung maka pangkatnya harus dikalikan
Contoh: $\left ( 5^{2} \right )^{3}=6^{2\times 3}=5^{6}$
Keempat:
$\left ( a\times b \right )^{m}=a^{m}\times b^{m}$>
Contoh: $\left ( 3\times 6 \right )^{2}=3^{2}\times 6^{2}$
Kelima:
Sifat yang ke lima ini, syaratnya “b” atau penyebutnya tidak boleh sama dengan nol (0).
Contoh:
Ke enam:
Pada sifat yang ke enam ini, apabila (an) dibawah itu bilangan positif, maka saat dipindahkan ke atas berubah menjadi negatif. Begitupun juga sebaliknya, apabila (an) dibawah itu adalah negatif, maka saat dipindahkan ke atas otomatis berubah menjadi positif. Mari kita lihat rumus dan contohnya berikut:
Ke tujuh:
Pada sifat yang ketujuh ini, kita bisa melihat bahwa terdapat akar n dari am. Apabila ketika disederhanakan, maka akar n akan menjadi penyebut dan akar m menjadi pembilang. Dengan syarat n harus lebih besar sama dengan 2. Contoh rumusnya: Ke delapan:
Bilangan eksponen nol seperti a = 1.
Contoh:
2 = 1
6 = 1
9 = 1
Syaratnya a tidak boleh sama dengan nol.
Ke Delapan sifat eksponen diatas harus kita pahami dan hafalkan, karena sifat-sifat eksponen tersebut adalah kunci untuk kita bisa mengerjakan soal-soal eksponen.
Fungsi Eksponen dan Grafiknya
Fungsi eksponen ialah pemetaan bilangan real x ke bilangan ax dengan a > 0 dan a ≠ 1. apabila a > dan a ≠ 1, x∈R maka f:(x) = ax kemudian disebut sebagai fungsi eksponen.
Fungsi eksponen, y = f(x) = ax : a > 0 dan a ≠ 1 mempunyai beberapa sifat-sifat sebagai berikut:
Contoh Soalnya:
Apabila f(x) =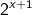 tentukanlah nilai dari f(3) dan f(-3)
tentukanlah nilai dari f(3) dan f(-3)
f(3) =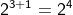 = 16
= 16
f(-3) =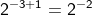 =
=  = 0,25
= 0,25
Bentuk-Bentuk Bilangan Eksponen
Didalam bilangan eksponen atau bilangan pangkat tidak selamanya selalu memiliki nilai bulat positif tetapi bisa juga bernilai nol, negatif maupun pecahan.
Bilangan Eksponen Nol (0)
Apabila a ≠ 0 maka a = 1 atau a tidak boleh sama dengan 0.
contoh:
3 =1
7 =1
128 =1
y =1
Bilangan Eksponen Negatif
Apabila m dan n merupakan bilangan bulat positif maka:
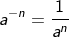
contoh:
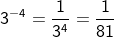
Bilangan Eksponen Pecahan
Rumus:
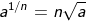
Contoh:
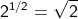
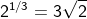
Bentuk Persamaan Eksponen
Bentuk persamaan eksponen ialah persamaan yang didalamnya terdapat pangkat-pangkat yang berbentuk sebagai fungsi dalam x yang mana x adalah sebagai bilangan peubah.
Rumus:
Artikel asli >
Read More
Bimbingan Belajar29. Bilangan Eksponen ialah bentuk suau bilangan perkalian dengan bilangan yang sama kemudian di ulang-ulang atau pengertian singkatnya adalah perkalian yang diulang-ulang.
Bilangan Eksponen biasa digunakan secara luas di berbagai bidang seperti: dalam bidang ekonomi, biologi, kimia, fisika, dan ilmu komputer dengan aplikasi seperti perbungaan, pertumbuhan jumlah penduduk, kinetika kimia, perilaku – perilaku gelombang dan kriptografi kunci publik atau ilmu yang mempelajari tentang bagaimana agar pesan atau dokumen seseoarang aman tidak terbaca oleh orang lain yang tidak berhak membacanya.
Contoh:
$a^{n}$ = a x a x a x…x a dikalikan sebanyak jumlah n
Contoh angkanya:
$2^{5}$ = 2x2x2x2x2 hasilnya 32
Sifat-Sifat Bilangan Eksponen
Terdapat beberapa sifat yang bisa kita ketahui didalam memahami bilangan eksponen yaitu di antaranya:
Pertama:
$a^{m}\times a^{n}=a^{m+n}$ apabila dikali maka pangkatnya harus ditambah
Contoh: $5^{2}\times 5^{3}=5^{2+3}=5^{5}$
Kedua:
$a^{m}\div a^{n}=a^{m-n}$ apabila dibagi maka sebaliknya pangkatnya harus dikurang
Contoh:
$5^{5}\div 5^{3}=5^{5-3}=5^{2}$
Ketiga:
$\left ( a^{m} \right )^{n}=a^{m\times n}$ apabila di dalam kurung maka pangkatnya harus dikalikan
Contoh: $\left ( 5^{2} \right )^{3}=6^{2\times 3}=5^{6}$
Keempat:
$\left ( a\times b \right )^{m}=a^{m}\times b^{m}$>
Contoh: $\left ( 3\times 6 \right )^{2}=3^{2}\times 6^{2}$
Kelima:
Sifat yang ke lima ini, syaratnya “b” atau penyebutnya tidak boleh sama dengan nol (0).
$\left ( \frac{a}{b} \right )^{m}=\frac{a^{m}}{b^{m}}$
$\left ( \frac{5}{3} \right )^{2}=\frac{5^{2}}{3^{2}}$
Ke enam:
Pada sifat yang ke enam ini, apabila (an) dibawah itu bilangan positif, maka saat dipindahkan ke atas berubah menjadi negatif. Begitupun juga sebaliknya, apabila (an) dibawah itu adalah negatif, maka saat dipindahkan ke atas otomatis berubah menjadi positif. Mari kita lihat rumus dan contohnya berikut:
Ke tujuh:
Pada sifat yang ketujuh ini, kita bisa melihat bahwa terdapat akar n dari am. Apabila ketika disederhanakan, maka akar n akan menjadi penyebut dan akar m menjadi pembilang. Dengan syarat n harus lebih besar sama dengan 2. Contoh rumusnya: Ke delapan:
Bilangan eksponen nol seperti a = 1.
Contoh:
2 = 1
6 = 1
9 = 1
Syaratnya a tidak boleh sama dengan nol.
Ke Delapan sifat eksponen diatas harus kita pahami dan hafalkan, karena sifat-sifat eksponen tersebut adalah kunci untuk kita bisa mengerjakan soal-soal eksponen.
Fungsi Eksponen dan Grafiknya
Fungsi eksponen ialah pemetaan bilangan real x ke bilangan ax dengan a > 0 dan a ≠ 1. apabila a > dan a ≠ 1, x∈R maka f:(x) = ax kemudian disebut sebagai fungsi eksponen.
Fungsi eksponen, y = f(x) = ax : a > 0 dan a ≠ 1 mempunyai beberapa sifat-sifat sebagai berikut:
- Kurva terletak di atas sumbu x (definit positif)
- Memotong sumbu y di titik ( 0,1 )
- Mempunyai asimtot datar y = 0 (sumbu x). Arti asimtot adalah garis yang tersebut sejajar dengan sumbu x.
- Grafik monoton naik untuk bilangan x > 1
- Grafik monoton turun untuk bilangan 0 < x < 1
Contoh Soalnya:
Apabila f(x) =
f(3) =
f(-3) =
Bentuk-Bentuk Bilangan Eksponen
Didalam bilangan eksponen atau bilangan pangkat tidak selamanya selalu memiliki nilai bulat positif tetapi bisa juga bernilai nol, negatif maupun pecahan.
Bilangan Eksponen Nol (0)
Apabila a ≠ 0 maka a = 1 atau a tidak boleh sama dengan 0.
contoh:
3 =1
7 =1
128 =1
y =1
Bilangan Eksponen Negatif
Apabila m dan n merupakan bilangan bulat positif maka:
contoh:
Bilangan Eksponen Pecahan
Rumus:
Contoh:
Bentuk Persamaan Eksponen
Bentuk persamaan eksponen ialah persamaan yang didalamnya terdapat pangkat-pangkat yang berbentuk sebagai fungsi dalam x yang mana x adalah sebagai bilangan peubah.
Rumus:
-
( Apabila
dengan a>0 dan a ≠0, maka f (x) = 0)
-
(Apabila
dengan a>0 dan a≠0, maka f(x) = p)
-
(Apabila
dengan a>0 dan a ≠0, maka f (x) = g(x))
-
(Apabila
dengan a>0 dan a ≠1, b>0 dan b ≠1, dan a≠b maka f(x) = 0)
-
+ C = 0 (Dengan
, maka bentuk persamaan tersebut dapat dirubah kedalam persamaan kuadrat:
+ Bp + C = 0)
Artikel asli >




